EE281-Electric Circuits

class: center, middle

# EE-281
# OPAMP Applications
# First-Order Circuits

## Ozan Keysan

[ozan.keysan.me](http://ozan.keysan.me)

Office: C-113 <span class="meta">•</span> Tel: 210 7586

---
# Capacitor Voltage & Current

# \\(i = C\frac{dV}{dt}\\)
--

# \\(V = \frac{1}{C} \int_0^t i(t) dt\\)

## Energy stored in a capacitor is:

# \\(w = \frac{1}{2} C V^2\\)

---
## DC Response

# \\(i = C\frac{dV}{dt}\\)
--

- ## Current of capacitor is zero if there's no change in the voltage (i.e. DC voltage)
--

- ## Capacitor voltage cannot be change instantenously as this means infinite current.

---
## Parallel Capacitors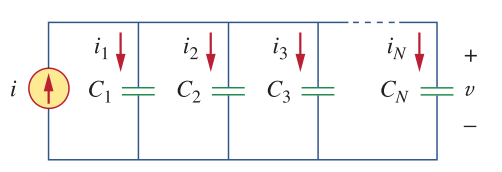

![](https://raw.githubusercontent.com/ozank/ee281/master/images/parallel_capacitor.png)
--

## \\(C_{eq} = C_1 + C_2 + C_3 ... + C_N\\)
---
# Series Capacitors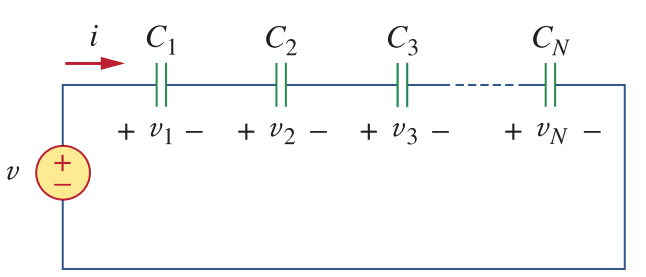
![](https://raw.githubusercontent.com/ozank/ee281/master/images/series_capacitors.png)
--

## \\(\frac{1}{C\_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} ... \frac{1}{C_N}\\)

---
# Series Capacitors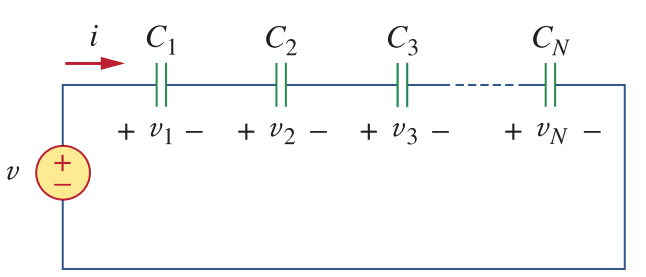
![](https://raw.githubusercontent.com/ozank/ee281/master/images/series_capacitors.png)

### For two capacitors
## \\(C_{eq} = \frac{C_1 C_2}{C_1 + C_2}\\)
---
# Inductors

# \\(V = L \frac{di}{dt}\\)
--

## \\(I = \frac{1}{L} \int_0^t V(t) dt\\)

--
### Energy stored in an inductor is:

# \\(w = \frac{1}{2} L I^2\\)

---
#DC Response
--

## - An inductor behaves like short-circuit under DC
--

## - Inductor current cannot be change instantenously as this means infinite voltage.

---
# Series Connection

Equivalent inductance of series connected inductors are the sum of inductances: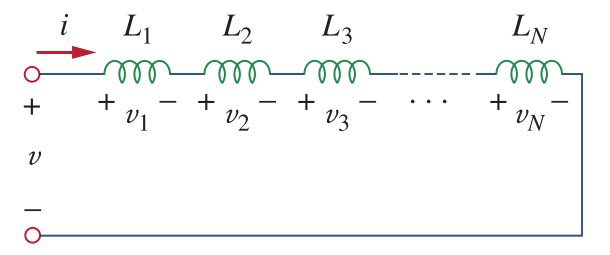

![](https://raw.githubusercontent.com/ozank/ee281/master/images/series_inductors.png)

## \\(L_{eq} = L_1 + L_2 + L_3 ... + L_N\\)

---
# Parallel Connection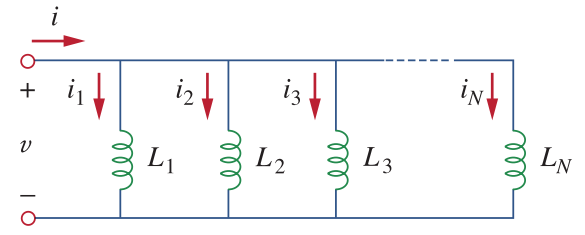

![](https://raw.githubusercontent.com/ozank/ee281/master/images/parallel_inductor.png)

## \\(\frac{1}{L\_{eq}} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} ... \frac{1}{L_N}\\)

---
# OPAMP Applications
## Analyze the circuit: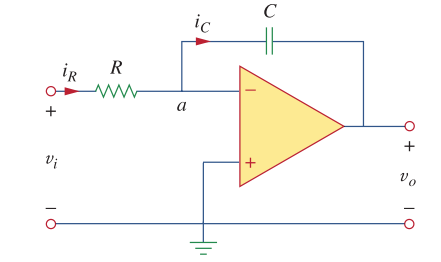

![](https://raw.githubusercontent.com/ozank/ee281/master/images/opamp_integrator.png)

---
# OPAMP Applications

### \\(i_R = i_C\\)

### \\(i_R = V_i/R\\)

### \\(i_C = -C d v_o /dt\\)

### \\(dv_o = -\frac{1}{RC}v_idt\\)

### Integrating both sides:

### \\(v_o = -\frac{1}{RC} \int_0^tv_i(t) dt\\)
---
# Integrator:

![](https://raw.githubusercontent.com/ozank/ee281/master/images/opamp_integrator.png)
---
# Exercise:
##Find the output voltage if:
### \\(v_1 = 10 cos (2t)~mV\\)
### \\(v_2 = 0.5t~mV\\)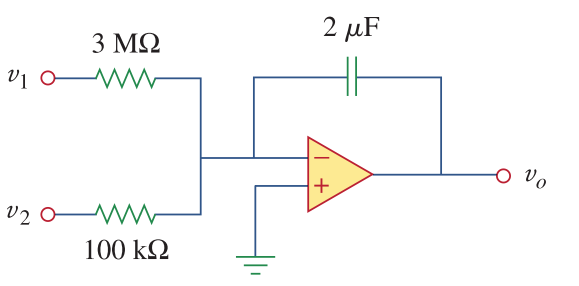

![](https://raw.githubusercontent.com/ozank/ee281/master/images/integrator_ex.png)
---
# OPAMP Applications
## Analyze the circuit: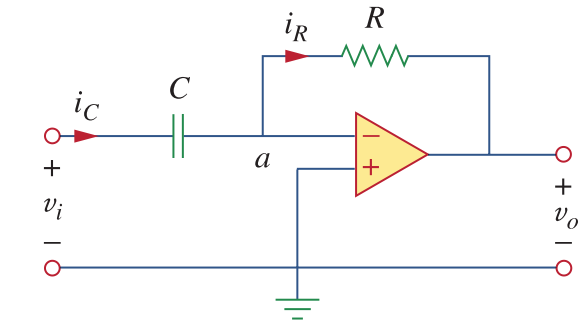

![](https://raw.githubusercontent.com/ozank/ee281/master/images/opamp_differentiator.png)

---
# OPAMP Applications

### \\(i_R = i_C\\)

### \\(i_R = - V_o/R\\)

### \\(i_C = -C d v_i /dt\\)

### \\(v_o = -RC dv_i(t)/dt\\)

---
# Differentiator

![](https://raw.githubusercontent.com/ozank/ee281/master/images/opamp_differentiator.png)

---
# Example

### Draw the output voltage if the input voltage is as follows:

![](https://raw.githubusercontent.com/ozank/ozank.github.io/master/presentations/images/opamp_differentiator_ex2.png)

---

# Any questions?

## You can download this presentation from: [keysan.me/ee281](http://keysan.me/ee281)